应用变量,从基础概念到实际案例

变量的应用：从基础概念到实际案例

在数学、科学、工程以及日常生活中，变量无处不在。变量是描述事物变化和关系的工具，它能够帮助我们理解和预测现实世界中的各种现象。本文将探讨变量的基础概念，并分析其在不同领域的应用。

一、变量的定义与分类

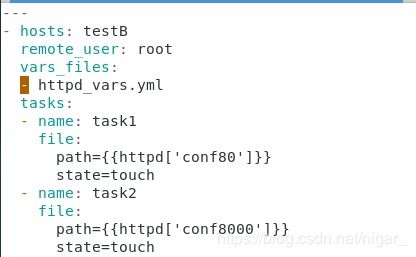
变量是指可以取不同数值的量。在数学中，变量通常用字母表示，如x、y、z等。根据变量的取值范围和性质，可以将变量分为以下几类：

离散变量：只能取有限个或可数无限个数值，如人的年龄、汽车的数量等。

连续变量：可以取无限多个数值，如温度、长度等。

随机变量：其取值依赖于随机事件，如掷骰子的点数、股票价格等。

二、变量的应用领域

变量在各个领域都有广泛的应用，以下列举几个典型领域：

三、数学领域

在数学领域，变量是构建数学模型的基础。通过引入变量，我们可以将实际问题转化为数学问题，并利用数学工具进行求解。例如，在求解一元二次方程时，我们引入变量x，将方程表示为ax^2 + bx + c = 0，然后利用求根公式求解x的值。

四、科学领域

在科学领域，变量用于描述实验结果和自然现象。科学家通过观察和测量，将实验结果表示为变量，并建立数学模型来解释这些现象。例如，在物理学中，牛顿第二定律F = ma中，F、m、a都是变量，分别表示力、质量和加速度。

五、工程领域

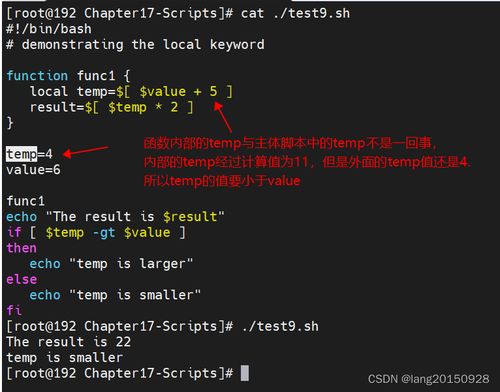
在工程领域，变量用于分析和设计各种工程系统。工程师通过建立数学模型，利用变量来描述系统的性能和约束条件。例如，在电路设计中，电阻、电容、电压等都是变量，工程师需要根据这些变量来设计电路，以满足特定性能要求。

六、日常生活

在日常生活中，变量也无处不在。例如，购物时考虑价格、质量、品牌等因素；烹饪时考虑食材、火候、调料等；旅行时考虑目的地、交通、住宿等。通过引入变量，我们可以更好地分析和决策，提高生活质量。

变量是描述事物变化和关系的工具，它在数学、科学、工程以及日常生活中都发挥着重要作用。通过掌握变量的基础概念和应用，我们可以更好地理解和解决实际问题。